
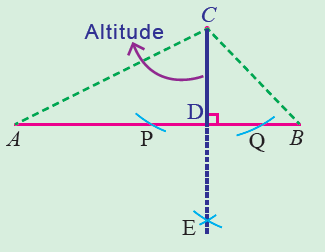
Construction of an altitude geometry full#
To draw a complete circle, continue drawing an arc until the pencil end of the compass makes a full circle back to point A. Then, move the pencil end counterclockwise to point B to construct arc AB. To draw a circle or arc, place the point end of the compass at a point, O, and place the pencil end of the compass at point A. Basic geometric constructionsĪ compass and straightedge can be used to draw many geometric figures and constructions. The straightedge or ruler to the right is used to draw line segments, but not to measure length. It can also be used to copy line segments. Geometric construction refers to the process of drawing lines, angles, and other geometric shapes and figures using only a compass and a straightedge (usually a ruler without measurements), without use of specific measurements of length, angle, etc.Ī normal or mechanical compass like the one shown above is used to draw circles and arcs. We observe that, in an isosceles triangle, the point of concurrence of medians (centroid) and altitudes (orthocentre) lie on a same straight line.Home / geometry / shape / geometric construction Geometric construction The point G is the centroid and point O is the orthocentre of ∆XYZ. Hence, ∆XYZ is the required triangle in which the medians XL, YK and ZU to the sides YZ, ZX and XY respectively intersect at G and altitudes XL, YM and ZN to the sides YZ, ZX and XY respectively intersect at O. With Q as centre and taking same radius, draw another arc that cut the previous arc at R. (xv) With P as centre and taking radius more than half of PQ, draw an arc. (xiv) With Z as centre and taking convenient radius, draw two arcs that intersect XY at P and Q. (xii) Draw the perpendicular bisector ST of the side XY that intersect XY at U. With F as centre and taking same radius, draw another arc that cut the previous arc at H. (x) With Z as centre and taking radius more than half of ZF, draw an arc. (ix) With Y as centre and taking convenient radius, draw two arcs that intersect ZX at Z and F. (vii) Draw the perpendicular bisector IJ of the side ZX that intersect ZX at K. With B as centre and taking same radius, draw another arc that cut the previous arc at C. (v) With A as centre and taking radius more than half of AB, draw an arc. (iv) With X as centre and taking convenient radius, draw two arcs that intersect YZ at A and B. (ii) Draw the perpendicular bisector DE of the side YZ that intersect YZ at L. Hence, ∆LMN is the required triangle in which the altitudes LI, MK and NJ to the sides MN, NL and ML respectively intersect at O. NJ is an altittude to the side ML produced. (xii) Join NC that intersect ML produced at J. With B as centre and taking same radius, draw another arc that intersect the previous arc at C. (xi) With A as centre and taking radius more than half of AB, draw an arc. (x) With N as centre and taking convenient radius, draw two arcs that intersect ML produced at A and B. (viii) Join MF that intersect NL produced at K. With E as centre and taking same radius, draw another arc that intersect the previous arc at F. (vii) With D as centre and taking radius more than half of DE, draw an arc. (vi) With M as centre and taking convenient radius, draw two arcs that intersect NL produced at D and E. With Q as centre and taking same radius, draw another arc that intersect the previous arc at R. (iii) With P as centre and taking radius more than half of PQ, draw an arc. (ii) With L as centre and taking convenient radius, draw two arcs that intersect MN at P and Q.


 0 kommentar(er)
0 kommentar(er)
